Last week a student was talking with me about what life would be like on a spinning space station. In the absence of a gravitational field, we can simulate a gravitational force with the centripetal force from the rotation of the space station. Famous examples of this principle include
O'Neill Cylinders and the ring-world in Halo
 |
| The Halo Ring-World |
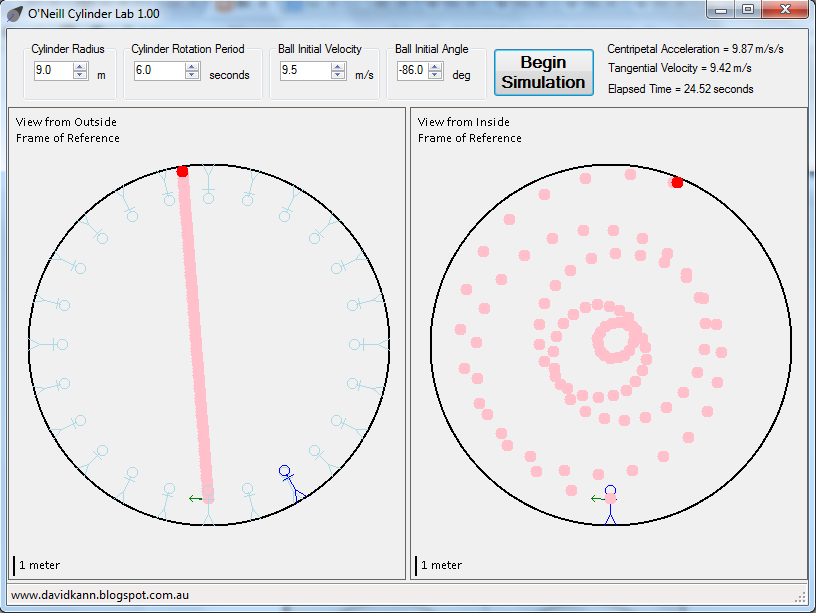
In our discussion we came across the thought of what it might look like to throw a ball in the air in a zero-gravity rotating space station. I was stumped so I brought the question to my colleagues. They were stumped. Eventually I was able to make a pair of parametric equations for position in time to model the motion of the ball but it didn't tell me much unless I could visualize the graph of the equations. The next logical step was to simulate the equations in software. Enter the
O'Neill Cylinder Simulator:
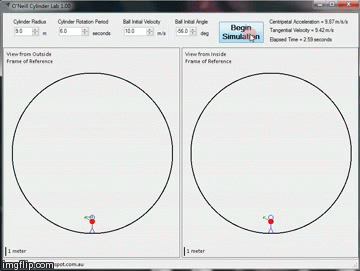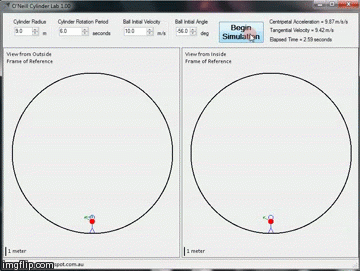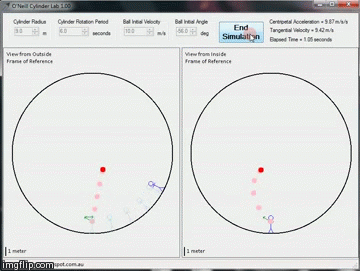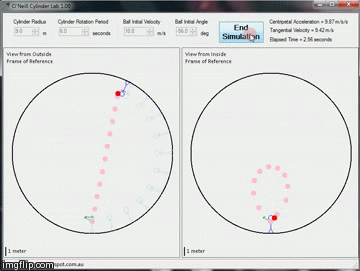 |
| Passing a Ball to Yourself in an O'Neill Cylinder |
When I saw the parametric equation animated (like above) it blew my mind a little. Here we see someone throwing a ball up and to the left, it circles above their head, and returns to them from the right. Throwing a ball in an O'Neill Cylinder apparently is nothing like on Earth. You can do some really sweet patterns:
 |
| A ball thrown through the center of the ring with a low velocity compared to the tangential velocity of the ring will spiral! |
Basically projectile motion is nothing like that on Earth. When Master Chief throws a grenade on Halo he might be in danger of it looping over his head and landing at his feet!
If you're curious, these are the parametric equations used to plot the position of the ball in both frames of reference
If you want the source code, you can grab it
here. Apologies in advance for the poor quality of code.






The effects described are very much related to scale. The animations depict a ball being thrown within a very small cylinder, where the path followed would indeed be very different to that on Earth.
ReplyDeleteGerard O'Neill (he of the O'Neill cylinder) proposed cylinders of about five miles diameter as suitable space habitats. At this scale, the effects on the motion of a thrown object would be pretty imperceptible. It's worth noting that even on the Earth there are effects due to the Earth's curvature and rotation - they're just too small to notice.
It's been observed that one clearly apparent effect of rotation in an O'Neill cylinder would be on waterfalls. A waterfall of any significant height would be visibly curved, even in a five-mile cylinder.
Very true!
DeleteIf you're curious to see how these effects scale, you can change the size and speed of rotation of the cylinder in the simulator. I chose a small default size to emphasize the effect.
I would love to see an animation of that waterfall!
This comment has been removed by the author.
ReplyDeleteThanks for sharing, David. I will share with my students.
ReplyDeleteHey awesome little simulator. The program maxes at 1000m diameter, but we need 6-8km for O'neils Island3 Colony. What part of the code would I update, I assume its nudsize, but I coulndt see where you maxed it at 1000m.
ReplyDeleteThanks!
DeleteIt's been a while since I had a look; I don't even have the right operating system for this program anymore! But looking back at the source I see this line in Form1.Designer.cs
this.nudRadius.Maximum = new decimal(new int[] {
1000,
0,
0,
0});
I would try changing that 1000 to 10000 to suit the sizes you wanted to test. At that size, though, I think the little guy will be very small on the screen!